Calling it a theory is definitely not pejorative.
One reason that science is difficult to understand among its non-practitioners is that it speaks a foreign language. As a prominent example, both distinct and subtle differences in denotation and connotation pull the word “theory” in manifold directions. The current Merriam-Webster online dictionary lists six different denotations, each with up to three subtly different shadings. It thus should come as no surprise that the word is understood differently outside the practice of science than inside and in multiple ways outside science.
Most English dictionaries list the most common scientific usage first and regard it as most frequent. In science the usual meaning is a set of general principles that explain how a system works. Examples are Darwin’s theory of evolution and the wave theory of light. Scientific usage of the word holds no hint of criticism. Even a faulty theory is better than none at all — as a source of hypotheses whose testing will reveal the faults and suggest improvements or replacements of the hypothesis and potentially of its underlying theory. Implicit in any scientific theory is that it will be tested against observations or experiments. In science a theory that cannot be tested should be discarded out of hand; it is a dead end in the road toward increased understanding, a fossilized context for extant observations.
The second definition usually listed is a set of general principles on which the practice of an activity is based. Music theory, for example, summarizes the methods and concepts that composers and other musicians use in creating music. Classroom practice may follow education theory. This kind of theory summarizes current and guides future practices within a field. This denotation grades toward the first only when the theory is at risk of being discredited on the basis of observations or experiments. Untested, decidedly unscientific, education theory is annoyingly ubiquitous. Some explanations of how science is supposed to work fall into this definition of theory.
A third definition is more frequently used within the practice of law, sometimes synonymously with “hypothesis” (again within law). It is an assumption made for the sake of argument or investigation. The defense lawyer is expected to have a different theory about what happened where, when and to whom than does the prosecutor. The theory is created to make the most favorable case for the client consistent with the facts as known so far. Lawyers are expected to speak pejoratively about theories they oppose. Implication of theory as potentially unfounded conjecture is strong. When a body of evidence for a theory of events and motives becomes convincing, it is no longer simply a theory, but transmutes toward “proof” of those events and motives.
Other, more rarely used meanings of “theory” also trend toward connotations of unsupported speculation. Transferring this connotation from non-science definitions of theory to science applications by critiquing a scientific theory as “just a theory” is specious. Scientific theories, analogous to legal ones, include explanations of already observed phenomena (facts in the legal case) and so have the evidentiary support of at least those phenomena. Scientific theories, however, are intended to be tested against further evidence. Overturn of a legal theory is a joyful event only for one side in the case. Overturn of a scientific theory (i.e., its replacement by something better) is a joyful advancement of knowledge in any case.
Darwin’s theory of evolution and the wave theory of light each had different shortcomings when first introduced. Many would argue that theories must identify a mechanism to be useful. Darwin’s theory of evolution is an excellent counterexample. It leapt over earlier theories by suggesting that the mean value of a trait like beak length in a bird was not under selection, but rather that individuals of a species that varied in expression of a trait underwent selection. Its second great leap based on observations of traits in closely related species among islands was to suggest that this selection could transform one species into another over time. Darwin realized that natural selection for variants in traits varied from place to place and over time. These inductive feats are all the more impressive because Darwin had no idea how variation in traits was produced or maintained from generation to generation or of the genetic code that underlay the reassortment of genes at fertilization. Rather than undermining Darwin’s theory, subsequent resolution of chromosomes, documentation of genetic recombination at fertilization and breaking of the genetic code have underscored the depth of Darwin’s insight by providing mechanisms. Although many good theories explicitly treat mechanisms from the start, Darwin’s is a clear example of an enduringly good one that did not when and as first articulated.
Although the fundamentals of Darwin’s theory of evolution have been buttressed by tests against evidence, it does not cover all circumstances equally well. Darwin implicitly assumed that resources limited populations of species, an assumption that more or less negates the possibility of rapid reproduction of favorable genes. Many populations, however, go through periods of rapid expansion, greatly accelerating their dominance by favorable genes. Understanding these genetic dynamics, recently named “natural reward,” is beginning to bridge well established understanding of individual mutations on the short time scale (microevolution) with the evolution of new species (macroevolution). It is helping to understand the pace of innovation in economic systems as well as in populations of organisms.
Christian Huygens (1629-1695) first proposed that light was a traveling wave. That theory explains many features of the propagation of light, namely refraction (bending of light at the interface between substances that differ in the speed at which light passes through them — as captured in their refractive indices) and reflection. Separation of white light into colored components by a prism is clearly explained and accurately predicted by Huygens’ theory. His contemporary, Isaac Newton, postulated that white light instead comprised particles of different colors, but his theory fell from use because Huygens’ made a much greater number of correct and useful predictions. Its applications included improved telescopes and eyeglasses. It fell to Einstein to resolve the fundamentally quantal nature of light as photons: Their quantal nature gives photons a wave-particle duality, with some behaviors more easily summarized by general theories for traveling waves and some behaviors understood only on the basis of discrete particles with discrete energy levels. Huygens and Newton were both partly right.
The range of application of a theory usually changes with tests of hypotheses, expanding with theory-derived hypotheses that are borne out, and contracting with hypotheses that are rejected based on testing. Applications of Darwin’s theory have shifted and increased their ranges, notably through the elucidation of Mendelian genetics and with the discovery of genetic coding in DNA. Both of these advances allowed new kinds of tests of Darwin’s big idea. Conversely, the range of application of the wave nature of light has been circumscribed by quantum theory. The quantal, particle nature of light is needed to understand, for example, how much energy a photon must have and how many photons it takes to be useful in photosynthetic conversion of carbon dioxide to organic carbon.
Diversity among useful theories makes the definition of a scientific theory unusually broad. I doubt that it is possible to be more specific in less fancy language than “a big idea from which testable hypotheses can be derived.” What makes some theories and associated hypotheses better than others is not so mysterious. Analogously with the three most important factors in determining the value of real estate (location, location, location), what determines the value of an idea and its hypotheses are prediction, prediction, prediction. That conclusion was drawn by Imré Lakatos, who grew curious about why some research programs made rapid progress as judged by rapid production of new knowledge and citations, whereas others faltered. He compared researchers in diverse fields of science but also compared the same researcher over time when he or she experienced distinct periods of recognized success and apparent failure. He found that successful labs (or in his British words research programmes) were working toward or from predictions. That is, they were developing new theory, using theory to derive hypotheses that made predictions, or testing such predictions. Lakatos is published in the same venues as other philosophers of science who more typically argue how science should work, but Lakatos instead was an empiricist who asked how science does work based on his observations of concrete examples.
But before distinguishing good from bad scientific hypotheses, it is worth revisiting the various meanings of “hypothesis.” Merriam-Webster lists the scientific meaning second: “a tentative assumption made in order to draw out and test its logical or empirical consequences.” It is expected that there will be no logical contradictions within a hypothesis or with its connection to theory (which itself contains no logical contradictions). Unresolved contradictions disqualify theories and hypotheses that contain them. Most important is the connection made to empirically testable consequences, i.e., testability of predictions. The first definition of “hypothesis” according to Merriam-Webster includes two additional, common applications of the word outside science: “(a) an assumption or concession made for the sake of argument or (b) an interpretation of a practical situation or condition taken as the ground for action.” Scientific hypotheses are purposed for empirical testing, not argument.
The third definition is “the antecedent clause of a conditional statement.” That’s another way of saying that a hypothesis is the “if” part of an if-then statement, such as the axioms that lead to a mathematical proof. I would add to these distinctions in meanings only a reminder that application of the first definition to law often carries a somewhat pejorative connotation as “just a hypothesis.” The word “hypothesis” carries no pejorative meaning in science.
Many other dictionaries list only a single definition of “hypothesis” and thereby suggest that a scientific definition is the only one or at least the primary one. For example, the Collins online dictionary gives “an idea which is suggested as a possible explanation for a particular situation or condition, but which has not yet been proved to be correct. The Cambridge online dictionary gives “an idea or explanation for something that is based on known facts but has not yet been proven.” The Cambridge dictionary provides better grammar with respect to the “which” versus “that” quandary, but from the scientific standpoint both definitions suffer from lack of emphasis on empirical consequences and from resort to concepts of proof that are based on discarded philosophies of science. Hypotheses are put out there to be tested against observations or experiments that support them, reject them or fail to be definitive. Moreover they remain hypotheses whether or not they are supported. It is possible, however, for a supported hypothesis over time to accrete bigger ideas and thereby to be elevated to the level of theory. The most useful definition of a scientific hypothesis is a deduction, based on a broader theory, that can be tested empirically.
Lakatos also articulated criteria for judging hypotheses, consonant with an emphasis on prediction and on practices in successful laboratories. It is easy to articulate multiple hypotheses in one’s subspecialty and to articulate hypotheses that use one’s favorite method, but chances are that a group of hypotheses developed this way will not be very well connected with each other and will provide neither strong support for, nor strong evidence against, an interesting, more encompassing idea (theory). Lakatos’ first criterion for evaluating a group of hypotheses to be tested thus is their generality and strength of connection to the overarching theory and their consistency with the theory and each other. Ad hoc hypotheses designed to explain away apparent anomalies in the theory are at the bottom of this heap. This connectedness-to-theory criterion is much easier to satisfy by deriving multiple hypotheses from a clearly articulated theory than by attempting to find a theoretical umbrella under which an aggregation of hypotheses can operate. Not surprisingly, the second criterion is that a hypothesis makes interesting predictions that can be tested. The third criterion is that at least some of the predictions are borne out. Predictions provide strong tests because they specify what to measure and in many cases how accurately and precisely it must be measured to resolve them from an alternative hypothesis. Utility of observations without this kind of guidance is much more limited.
One can argue whether intelligent design (ID) is a theory or a hypothesis. First, ID is more about not having hypotheses than about having them. To quote an ID website, ID "holds that certain features of the universe and of living things are best explained by an intelligent cause rather than an undirected process such as natural selection." It is recognized by the "lack of any known law that can explain" seemingly purposeful design. As an aside, purposeful design is not the subject of any scientific law. Proponents of ID take deliberate advantage of lay misunderstanding of scientific usage regarding laws, theories and hypotheses. Intelligent design is religious speculation or assertion. It is not in any sense an alternative to the scientific theory of evolution that continues to make many interesting predictions, many of which are found to be accurate. Lack of fit to the predictions has been even more informative in improving more sophisticated and mechanistic theories of evolution. The only evolution evident in ID theory is continual refining of its semantic obfuscation aimed at the layperson. ID makes no testable predictions and provides no scientific honesty in the form of observations that would overturn its theory that structures such as bacterial flagellar motors and image-forming eyes are too complicated to have been produced by other than a supernatural power. ID is teleological by its own admission and tautological in practice.
"The belief that science proceeds from observation to theory is still so widely and so firmly held that my denial of it is often met with incredulity. I have even been suspected of being insincere—of denying what nobody in his senses would doubt."
"But in fact the belief that we can start with pure observation alone, without anything in the nature of a theory is absurd; as may be illustrated by the story of the man who dedicated his life to natural science, wrote down everything he could observe, and bequeathed his priceless collection of observations to the Royal Society to be used as evidence. This story should show us that though beetles may profitably be collected, observations may not." ~Sir Karl R. Popper
One criterion sometimes suggested for judging theories and hypotheses is known as Ockham’s razor. William of Ockham (15 miles south of Heathrow airport, and still a small town) was ordained in the Franciscan order in 1306 CE. Before he could complete his studies in theology at Oxford, in 1323 CE he was summoned to the papal court for blasphemy associated with his torpedoing of the medieval synthesis of faith and reason attempted by Thomas Aquinas. He self identified as a philosopher, a keen student of Aristotle, a political activist against the corrupt Pope, but not as a scientist. His razor is equated in science applications with the principle that if two theories account for known facts and phenomena equally well, the simpler one is better. The practice of science, however, advances from predictions and aims toward currently unknown outcomes of additional observations and experiments: If two theories account for known facts and phenomena equally well, choose the one that makes predictions, and makes better predictions, even if it is more complicated. Don’t let the razor cut off discovery.
That said, however, it is entirely possible for a simpler theory to make better predictions. Elliptical planetary trajectories around the sun, for example, provide much simpler descriptions and more accurate predictions than Ptolemy’s epicycles around the earth. And a theory can collect a large and complex suite of exceptions through repeated modifications, based on rejected hypotheses, to a point that motivates the search for a simpler theory. A related concept is elegance of a theory. Its difficulty in application as a criterion is that scientific elegance is easier to recognize than to define objectively. Prime criteria for the value of a theory are how fundamental it is to understanding and how broadly it applies, i.e., its depth and breadth. Elegance often involves embodiment in a simple but highly evocative equation.
Two other terms (besides hypothesis and theory) are applied to subsets of scientific ideas, albeit less frequently — law and rule. What is called a law or a rule in science is clearly more arbitrary than denotations of theory or hypothesis. In science, laws form a subset of theories, ones that are not in dispute (are well supported over a long period by evidence) and can be phrased succinctly in either words or an equation. Newton’s second law of motion, for example, states that for an object of constant rest mass (m), force (F) acting on an object is equal to its resting mass times its acceleration (a). More intuitively, the change in its momentum (momentum being mass times velocity, v) equals the force applied:
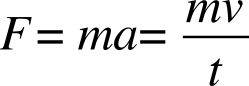
Calling a theory a law does not imply universal applicability. This one applies neither at atomic scale, where quantum effects act, nor at speeds where relativistic effects become important.
Newton’s first and third laws of motion by contrast are more generally and effectively given as simple statements than in equations: Every object persists in its state of rest or uniform motion in a straight line unless it is compelled to change that state by forces impressed on it; and, for every action, there is an equal and opposite reaction.
Newton’s law of gravitation, in turn, states that the force of gravity acting on each of two bodies (each with a mass, m, differentiated by the subscripts 1 and 2) is equal in magnitude, opposite in direction and proportional to the product of their masses, and inversely proportional to the square of the distance (d ) between their centers of mass:
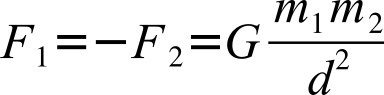
Both of the proportionalities are scaled by the gravitational constant (G). Because the forces are equal, the smaller mass will experience a greater acceleration, as the second law of motion dictates. The negative sign reflects the opposition of equal forces expected from the third law of motion.
When Newton first wrote the equation for gravitational force, it was very much a theory with limited empirical support. Newton had little idea what the force was, but his first law of motion asserted that something attracted the apocryphal apple and everything else toward Earth’s center. The inverse square relation (d squared in the denominator) and the product of masses in the numerator) were postulated on the basis of planetary motions. The value of G was first estimated over a century after Newton published the theory. Discovery of Neptune depended on previously unexplained motions of Uranus, demonstrating the power of the theory. It became known as a law, but it was insufficient to explain Mercury’s orbit and was supplanted by general relativity. Nevertheless, it is still known as a law.
Not all theories that meet both criteria (by being or having been durable and succinct) are called laws. Einstein’s theory of conversion between mass and energy is succinct and has been durable, yet has not been called a law. It is simple (containing only three terms, one with an exponent). It is horrifying (in terms of potential for release of energy) but also elegant, indicating that energy (E ) can be released in proportion to an object’s rest mass (m) and the square of the speed of light in a vacuum (c ):
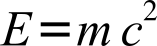
In short, laws are theories that are succinct and that held sway for long periods and may still hold sway, but not all theories that have met these two criteria are called laws. The distinction between a law and a theory is of greater interest to a philosopher or a lawyer than to a scientist.
Things called rules are weaker relationships than things called laws in science. Applications of “rule” as a label are certainly rarer in science than applications of “law.” I don’t know any scientists who choose among theories by worrying whether they are called theories, laws or rules. For that matter, I don’t know of any scientist who distinguishes theories from laws or rules. In the vernacular and the legal profession, a big difference is in the consequences of breaking a rule versus a law. Rules are rare as labels in science. Cope’s rule is among the most prominent and refers to the statistical tendency, during evolution within a lineage, for body size to increase. Cope’s rule refers to a statistical regularity; it is not a theory in the sense of providing an explanation or prediction except for predicting that because the pattern has been observed in many lineages it is likely to be observed in others. Articulation of the rule preceded potential explanations, which remain unresolved.
In science, breaking laws and rules demands attention rather than punishment. Adding to confusion, “The exception proves the rule” has reversed meaning over time in the vernacular. The archaic definition of “to prove” equates with “to test.” The intention of the original definition was that an exception was a test result that negated the rule. The phrase has come to mean instead that a few exceptions are to be expected or even desired of a sound rule, and that instead a rule lacking exceptions should be suspect. The situation is, “Highly illogical,” to quote Spock. In my view, science usage in describing its methods would be improved by global replacement of proof and prove by “test.”
Last but not least in the lexicon of scientific means of prediction is the model. An exercise left to the reader is to work (in the case of the online Merriam-Webster dictionary) through the fourteen noun, seven verb and two adjective definitions of “model.” I don't try here because I find little confusion of the scientific applications of the term with applications elsewhere. Here I focus on the three most frequent denotations used by scientists. Any attempt to describe models in scientific application needs to be preceded by a clear declaration that no model is expected to fully reproduce the reality that it is intended to represent. Models intentionally simplify to reveal whether excluded details matter. Whether they do or not, knowing the result advances progress. If the fit is good, the model is useful in allowing simplified prediction and potentially measurement. If the fit is poor, something important is missing from the model or something was included that should be missing. It is sometimes argued that if the fit is good the model is not a simplification. At most that argument applies only to the process that is well duplicated by the model and ignores the benefits of excluding all the other details.
"Since all models are wrong the scientist cannot obtain a 'correct' one by excessive elaboration…Just as the ability to devise simple but evocative models is the signature of the great scientist so overelaboration and overparameterization is often the mark of mediocrity…Since all models are wrong the scientist must be alert to what is importantly wrong. It is inappropriate to be concerned about mice when there are tigers abroad." ~George E. P. Box
The most familiar definition by far is the top entry in most dictionaries as a representation of something, usually by fastidious duplication of structural features, and usually at a reduced scale. Most of us grew up with model planes, trains, cars and even the visible man or woman. It makes good sense to examine feasibility and practicality in a small version before building, or (in the case of surgery) operating upon, the subject at full scale. Physicists have identified ways to scale experiments with small models by adjusting flow speed, fluid viscosity and fluid density such that results of important measurements, for example drag on a car body or ship hull, can apply at full scale. I can put a small model in a flow tank and use measurements on and around it to predict the same quantities on an object at full scale. Although miniatures are most common as models, these scaling approaches are also used by scientists with larger-than-life models in order to understand flows around microscopic organisms and how, for example, they can capture small suspended particles such as aquatic bacteria as flows go by. The diversity of problems addressed with physical models below, at, and above natural scale has exploded with the advent of robotic models that simulate active behaviors to address issues such as exactly how wings are deployed in hovering.
Also frequent in scientific applications ideas and practices of quantitative modeling, which grow ever more prevalent and diverse with expanding computing power. They range from statistical correlations such as those of Cope’s rule, with limited predictive power (in the case of Cope’s rule that the next lineage examined will show a similar trend) to evokative, mechanistic equations such as the three above. Computer models that incorporate the current state of a system at many points in space and use a set of rules to predict changes at those points over the next time interval are increasingly used as tests of those rules. Questions that in the early days of my career required construction of a special flow tank and physical model of an organism or its component structures to assess effects of flow past an animal and took days to execute and measure can be simulated and run in a computer within an hour. Modifications to look at effects of added features like spines can be carried out in minutes.
Less frequent is the definition of a third kind of model, most often called an “animal model,” referring to a situation in which tests of effects on an individual of one species are used to predict effects of the same stimulus on individuals of another species. This practice has been around long and frequently enough, however, to engender its own vernacular, that of the “guinea pig,” although the use of laboratory-reared mice and rats is far more widespread. Animal models are used to reduce, but not eliminate ethical issues in medical and veterinary contexts, such as in the testing of vaccines. The idea generalizes somewhat to situations where the target organism is difficult to capture or culture or where the model has some feature that makes it more amenable to research. Escherichia coli (more often listed simply as E. coli ) has been used as a model for other bacteria that are harder to culture, for example in experiments assessing how bacteria swim. The common fruit fly (Drosophila melanogaster ) initially served as an animal model because its chromosomes are unusually large and easy to observe, and a whole colony could be reared in a small space on a single banana. Its value as a model has only increased as the large numbers of genes it shares with other animals have been documented. Arabidopsis thaliana, rockcress, analogously serves as a model for plant genetics and development. As for any model, an important question is how well the model species represents the species (singular or plural) for which it serves as model.
Box, G. E. P. 1976. Science and statistics. Journal of the American Statistical Association 71: 791–799.
Lakatos, I., 1968, January. Criticism and the methodology of scientific research programmes. Proceedings of the Aristotelian Society 69: 149-186.
Lakatos, I. 1970. Falsification and the methodology of research programmes. Pp. 91-196 in I. Lakatos and A. Musgrave, Eds. Criticism and the Growth of Knowledge. Cambridge Univ. Press (Proceedings of the International Colloquium in the Philosophy of Science, London 1965, volume 4).
Popper, K. 1963. Conjectures and Refutations: The Growth of Scientific Knowledge. Routledge, London.

Comments